Tacheometric Surveying - Definition, Principle, Advantages, Methods

What is tacheometric surveying?

The definition of tacheometry we can give as follows

It is branch of surveying which deal with various measurements like vertical distance and horizontal distance that is measured indirectly from taking only instrumental observation.

We conduct Survey is to prepare contour map of site. We can also use it for knowing elevation of highway or railway.

In this survey We calculate RL of various point from taking reading and by some observation.

Principle of Tacheometry

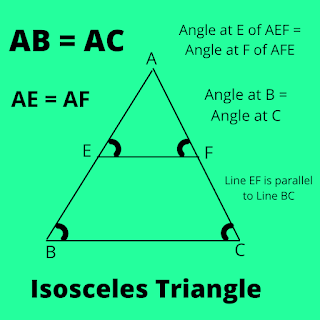
The main principle of Tacheometry is based on the basic principle of isosceles triangle.

In any two side equal triangle means isosceles triangle, there is one property which is used in the Tacheometry.

It state that

Ratio of the perpendicular to vertex on their base and their base is always constant in isosceles triangle.

It means if object is far from vertex than it cover more area and if it is near than it cover less area because ratio is constant.

In other words,

For example, this is a Triangle ABC.

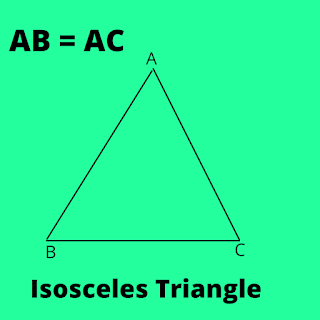
Suppose, Triangle ABC has two sides AB and AC are equals. Means AB = AC.

So, Triangle ABC is Isosceles Triangle.

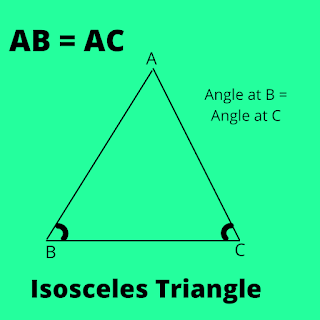
Now, because it has AB = AC, angle at point B will also equals to angle at point C, by the property of it.

Now, let's draw line EF parallel to line BC in this Triangle such as both of its end will remains on side.

Now, because line EF is parallel to line BC, and AB = AC; so Triangle AEF will also be isosceles Triangle with AE = AF.

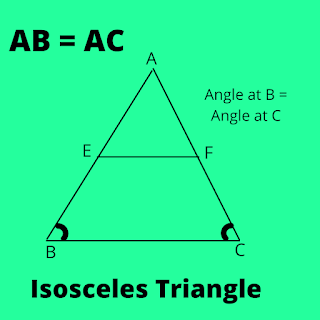
Also, Angle at E of AEF = Angle at E of AFE

So, by property of it,

Ratio of AE and AB will be equals to ratio of AF and AC.

AE/AB = AF/AC

Also,

EF/BC = AE/AB = AF/AC

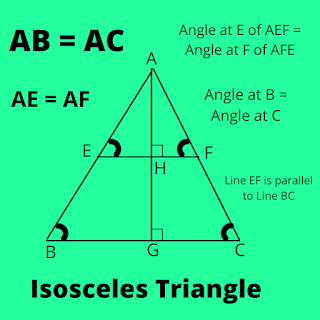
Now, if we draw a line Perpendicular to line BC from point A. And call it line AG, which intersect at point H on line EF.

Here, AH is perpendicular, means it makes 90° angle with line EF.

And AG is perpendicular to BC, as it makes 90° with line BC.

So, here,

AH/EF = AG/BC

So, whatever place we draw a line in between it, ratio will remains same.

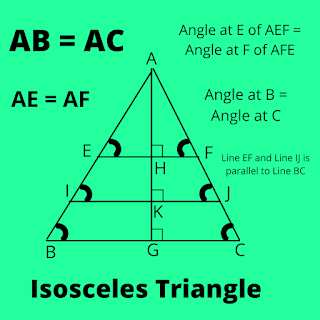
For example, we draw, IJ line, parallel to BC.

Then here also,

AH/EF = AK/IJ = AG/BC

So, whenever this point is parallel to line BC, its ratio of it will be same.

From this, 

Suppose we have AH, EF, and AG.

So, we can find BC as,

BC = (AG*EF)/AH

By this principle, Tacheometer works.

There is object which is far from instrument but if we take reading in instrument then it appears as low distance in diaphragm.

Advantages of Tacheometric surveying

• It is not necessary to do chain operation which is required in other method of surveying.
• We can do survey in area like Hill and mountain where it is very difficult to do survey by other methods.
• If we not need very high standards and accuracy then this is right method.
• It require low amount of time compare to other ways of surveying.
• Because Tacheometry is indirect method that we do not require some instrument that is necessary in plan table surveying or in theodolite surveying.

Generally we use this survey when we do not require to have high accuracy in our observation.

Uses of tacheometry

Tacheometry have many applications like below.

It's usefulness is due to fact that it does not need chaining or horizontal measurement.

• We can use it for preparation of contour map in case when both horizontal and vertical distances needed.
• It is very useful for triangulation surveying also.
• Sometimes work of surveying is in difficult areas when we cannot use some direct methods like Theodolite traversing or plane table surveying.
• Tacheometry is reconnaissance survey for highways, roadways and railways.
• We can use it as establishment of secondary control points.

Method of Tacheometric surveying

There is basically two method and one of this method is further classified into sub methods.

Main two classification are as follow:

1. Stadia Method
2. Tangential Method

This classification is based on taking observation.

The first classifications stadia Method which is further divided into two parts which is as below.

1. Movable hair method
2. Fix hair method

From using this methods we can calculate RL, elevation and horizontal distance.

Usually, we prefer the fix hair method because it consume less time compare to movable hair method.

Click to ZOOM.

You can see theory of stadia Tacheometry in above image.

This methods is very useful to determine various information and taking readings to know details of various measurements.

Now, let's see more detail about the method.

First let see Stadia method.

Stadia method of Tacheometry

Almost all survey is based on stadia method because it is easy and convenient. 

In this method we use theodolite which has three hair on it.

It is usually done by stadia rod.

There is two subtype as we see which is as follows. 

1. Fixed hair method

Measurements taken is upper hair reading, lower hair reading and verticle angle.

Hair is kept fixed and we take reading on staff.

After Calculate horizontal distance from following formula.

             H = AS+B

Here, vertical angle is zero.

H is horizontal distance. 

A is multiplying constant.

B is addictive constant.

And 

S = upper reading - lower reading (on staff)

However, this formula is only apply if vertical angle is zero.

Or we can say it only apply if

V = 0

But sometimes we need formula for which V is not equal to zero.

Like a situation in mountain.

Or hilly areas.

When there is slope and some vertical distance above horizontal line then there is other formula which even apply if angle is negative.

Formula for horizontal distance when V is not equal to zero

As we know, it is for some angle to horizontal line.

Let, angle is x

H is horizontal distance

A and B is multiplying and addictive constant.

Here, angle is available.

So, we take help of trigonometry to this equation.

And the equation have function like cosine and cosine square.

The formula is..

H = A (cos^2 x) S + B cos x

Here vertical distance is as follow:

V = H tan x

Because

tan x = V/H

Therefore,

V = A (sin x *cos x) S + B sin x

This is fundamental formula for tacheometry which is used almost all calculations.

Just remember formula for H and after you find V by calculating...
 H tan x

In some calculations, ask for RF then draw diagram or figure.

Figure make work easy and fast to calculate for this type of problems.

Instruments

• Tacheometer

• Staff