Latitude and Departure in Surveying - Formula, Explanation, Examples
In this article, we will see about Latitude and Departure in Surveying, what are they, how we can derive formula for it, Sign Convention, and Some Examples.
So, Let's see,
What are the Latitude and Departure?
Latitude of a Line is a Projection of a given Line on N-S Line.
Departure of a Line is a Projection of a given line on E-W Line.
What does it means?
In simple words,
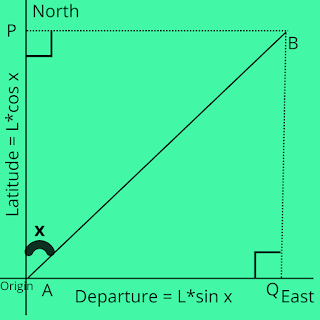
Suppose we have a Line AB.
Now this line can be anywhere. But for projection, it's one endpoint should be on Origin.
So, let's take point A to Origin O on North-East-South-West plane, such as line remains as it is, but one point A will be on Origin.
Or Alternatively, we can also make N-S-W-E plane, and can make origin at a point there without taking line away. So, let's see,
As you can see, line AB, which point A at origin. Right Side of Point A is East Direction, left side West Direction, Up side North Direction, and down side South Direction.
So, when we project like on North-South axis. It means we take other point on Line which is far away from Origin, and draw perpendicular line with respect to North-South, place where line intersect on North-South axis, and place of origin; distance between these two, or line whose end points are these two, is called by Latitude.
Here's Example:
Point B on Line AB intersect North-South axis at point P, which is perpendicular as we can see.
So, Line PA will be projection of line AB on N-S axis, and therefore it will be Latitude.
We can understand about Departure in the same way. But here replacing North-South to East-West axis. Projection of line on E-W axis, will be Departure of line.
For example, as we have seen diagram, departure for it will be AQ, where Q will be point which intersect perpendicularly with E-W axis.
Here's Latitude and Departure both for Line AB:
Now, let's see,
Formula - How can it be Derived?
Triangle APB, and Triangle AQB are Right Angle Triangle.
L = Length of Line AB
x = angle between line AP and line AB
And because line AP and BQ are parallel, angle ABQ or angle between line AB or line BQ will also be x.
Now,
cos x = AP/AB
sin x = BP/AB
and,
cos x = BQ/AB
sin x = AQ/AB
As here, AP = BQ; and PB = AQ.
As we know AP is Latitude and AQ is Departure.
So,
AP = AB * cos x = L * cos x
and;
AQ = AB * sin x = L * sin x
Therefore,
Latitude l = L * cos x
Departure d = L * sin x
Related Formulas
Given l and d of a Line, L is:
L = √(Latitude2 + Departure2) = √(l2 + d2)
Given l, and d of a line; x is,
x = tan-1(Departure/Latitude) = tan-1(l/d)
Ratio of l to L is,
l/L = cos x
Ratio of d to L is,
d/L = sin x
Given L, and l; angle x is:
x = cos-1(l/L)
Given d and L, we can find x as:
x = sin-1(d/L)
Given l, and angle x, we can find L as:
L = l*sec x = l/(cos x)
Given d, and x, we can find L as:
L = d*cosec x = d/(sin x)
Given l, and x; we can find d as,
d = l*(tan x) = l/(cot x)
Given Departure of a line d, and Angle x, we can find Latitude l as;
l = d*(cot x) = d/(tan x)
Ratio of d to l is:
d/l = tan x
Ratio of l to d is:
l/d = cot x
Given L, and l; d is:
d = √(L2 - l2)
Given d, and L; l is:
l = √(L2 - d2)
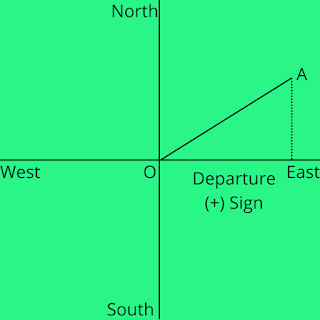
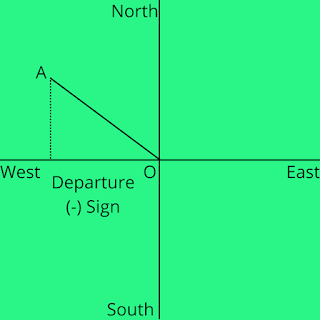
Sign Convention
Examples
Q (2): What will be ratio of Length of Line to Latitude of that line?
A: sec x, or sec (Angle between Line and North)
Hint: As latitude l = L*cos x ,
(Length)/(Latitude) = (L)/(l) = sec x
Q (3): What will be ratio of Departure to Length of Line?
A: sin x
Hint: As Departure, d = L * sin x;
Departure/(Length of line) = (d)/(L) = sin x
Q(4): If Length of line PQ = 50m, If latitude of that line is 25m; then What angle does it makes with North?
A: Either 60° or 300°
Hint: As l = L * cos x ; x = cos-1(l/L)
So, x = cos-1(25/50) = cos-1(0.5) = 60°
Now, cosine function can be positive in first or forth quadrants, here's if it makes angle of (360 - 60)° = 300°, then also cos(300°) = 0.5; so it could be either of 60° or 300°
Q (5): If Length of Line PQ is 50m, and Latitude of a Line PQ is 35.36m, and line PQ is in First Quadrant, then what would be Departure of that line ?
A: 35.36m
Hint: cos x = l/L;
x = cos-1(35.36/50)
x = cos-1(0.7071)
x = 45° or (360 - 45)°
Now, as line PQ is in first Quadrant, x = 45°.
Now, d = L * sin x = L * sin (45°)
So, d = 50 * (0.7071) = 35.36m
Q (6): If Latitude of a Line CD is 30m, and Departure of line CD is 30m, then what will be the value of Length of that line?
A: 42.43m
Hint: As,
l2 + d2 = L2
So, L = √(l2 + d2)
So, L = √((30)2 + (30)2)
So, Length of Line CD; L = 42.43m
Q (7): What will be l and d of a Line whose Length L is 35m, and Angle it makes with North x is 30°?
A: l = 30.31m ; d = 17.5m
Hint: l = L*cos x = 35 * cos (30°) = 35 * (0.866) = 30.31m
d = L*sin x = 35 * sin (30°) = 35 * (0.5) = 17.5m
Q (8): What will be ratio of l to d, for a line which makes angle with North as 45°?
A: l/d = 1
Hint: l/d = tan x = tan 45° = 1
Q (9): What will be ratio of L to l, for a line whose angle with North is 60°?
A: L/l = 2
Hint: L/l = sec x = sec 60° = 2
Q (10): If l = 12m, and d = 9m, what will be Length L of that line?
A: 15m
Hint: L = √(l2 + d2) = √(122 + 92) = 15
Q (11): If l of line AB is 15m, and l of line CD is 20m; but both lines AB and CD makes the same angle x with North, then what will be ratio of Length of Line AB and of Line CD?
A: Ratio will be 3:4
Hint: As l = L*cos x
So, lAB = LAB*cos xAB
and, lCD = LCD*cos xCD
Now, xAB = xCD
So, cos xAB = cos xCD
Therefore ratio of LAB to LCD, will be,
LAB/LCD = lAB/lCD = 15/20 = 3/4 or 3:4
Q (12): If d of a line is 30m, and L of the line is 50m, what will be l of same line?
A: 40m
Hint: As l = √(L2 - d2) = √(502 - 302) = √(2500 - 900) = √(1600) = √(40*40) = √(402) = 40m
Some More Exercise
Q (1): The Ratio of Length of three lines AB, CD, and EF is 3:4:5. Angles all three lines makes with North or Bearing of it, are same. Then What will be ratio of Latitude of a line AB, CD, and EF?
A: Ratio of Latitude will be 3:4:5
Hint: If Angle x is same, then Latitude of Line will be Proportional to its Length for a set of lines, from formula, l = L*cos x.
Now,
LAB:LCD:LEF = 3:4:5,
and for all lines, angle x is same, so cos x will be same.
So,
lAB:lCD:lEF = 3:4:5
Q (2): If Length of a Line is 70m, and Bearing or Angle it makes with North, x is 60°, then what will be its Latitude l?
A: 35m
Hint: l = L*cos x = (70)*cos 60° = (70)*0.5 = 35m
Q (3): Departure of five lines AB, CD, EF, GH, IJ are 10m, 20m, 30m, 40m, and 50m. If angle each lines makes with north is 30°, then what will be the Length of Each Line?
A: LAB = 20m, LCD = 40m, LEF = 60m, LGH = 80m, and LIJ = 100m
Hint: L = d*cosec x,
Now, x = 30°,
So, cosec x = cosec 30° = 2,
Therefore,
LAB = 10*2 = 20m,
LCD = 20*2 = 40m,
LEF = 30*2 = 60m,
LGH = 40*2 = 80m,
LIJ = 50*2 = 100m
Q (4): If Length of a Line L is 100m, and latitude of a line is 80m, what will be its Departure?
A: 60m
Hint: d = √(L2 - l2) = √(1002 - 802) = √(10000 - 6400) = √(3600) = 60m













Comments
Post a Comment