Errors in Surveying - What is it, and Examples

In this article, we will see about What error is, what are its types, how can we minimize it, and some examples.

What are the Errors?

Errors means difference of measured value of quantity and of actual value of quantity.

For example,

Suppose, we have a line AB in the field.

Its actual value is 20m, means point A is 20m far away from point B.

Now, we try to measure line AB. And due to some reasons, we measure it as 19m. So, here is Error of 1m in absolute terms.

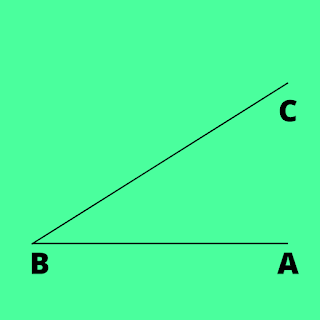
Other Example:

Suppose we have a Angle ABC, which is angle between line AB and line BC, at point B. 

Suppose  value of Angle ABC at point B is 30°.

Then, we measure Angle ABC at point B, as 29°.

So, absolute error is |29° - 30°| = 1°.

Suppose instead of measuring 29°, if we would have measured it as 32°, then it would be of |32° - 30°| = 2°.

Another Example,

Suppose a Person measure the height of a Tower.

To measure it, he use some Instruments, and take readings. He is far away from tower, and to calculate its height, as he measure angle and other required readings. He then use formulas of Trigonometry to compute the required Height. He arrived at height as 18m by his calculations.

If real height of a Tower is 20m, then absolute Error is |18 - 20| = 2m.

Various Types

Personal Error

Errors in our Observation can be because we made mistake.

For Example, Suppose a person measure line CD with a chain. And he does not set it like as straight, but somewhat more curved. 

So, what readings will be on chain, will have some error, as it does not accurately measure line CD.

Another Example,

Suppose a Person takes observation with a Theodolite. But he does not center it, or level it, and also while taking readings, he used wrong part to measure the observation. So, there may be some errors in it.

Instrumental Error

Another way, errors can occurs is due to some problems in Equipment or Tools.

In Surveying, we use equipment like:

• Theodolite
• Plane Table 
• Alidade, 
• Chain, 
• Total Station, and 
• Some Modern Instruments.

Now, as there can be some problems in Instrument, so whenever we take readings with it, it gives different values than actual value.

For example,

Suppose with a Theodolite, we measure Angle. And there is some problem in Theodolite because of which, it gives us 2° more than what actual value is. So, every time we measure, we get 2° more value in this case.

Other Example,

Suppose we have a Chain. Length of Chain is written as 10m, but actual value of chain is 9.9m. So, here is problem with Chain as instead of measuring 10m, every time it measure 9.9m. So, if we measure 20m with a Chain, the actual value is 19.8m, as for every 10m, there is measuring done of 9.9m.

Natural Error

Another type of error also can occur. 

For example, 

There can be some unknown reason, or mix of various types of causes related to atmosphere or curvature of Earth, and of nature. 

It can cause our observations to be different than what should it be. We can call it, natural error or random error.

How can we minimize Errors in Surveying?

• We can hire skilled Person, who has experience.
• By taking careful readings, careful calculations, and careful judgements.
• By noting places where mistakes, miscalculations, or fallacy can occur.
• By calibrating our Instruments.
• By taking same measurements many times, or taking same measurements in different ways.
• By using better, modern Instruments.
• By using different methods, or methods having more accuracy, and less error-prone.
• By understanding sources of errors.
• By measuring in clean Atmosphere, when almost no rain or much wind is there.
• By noting down Temperature. And if its deviated from standard Temperature, adjusting for it.
• By doing field work in a standard manner.

Formula

 

(e = Error)

e = Measured Value - Actual Value

 

So, 

Actual Value = Measured Value - e

 

and,

Measured Value = Actual Value + e

 

In our field work, many times there is more than one types of error or more than one error.

There are different methods for how we can find total errors due to it, and what would be its combined effect.

Correction

If we have measured value, we can find its true or actual value by adding "Correction".

So, 

Actual Value of Quantity = Measured Value of Quantity + Correction

There are different formulas to calculate error occur due to:

• Refraction in atmosphere, 
• Sag in Tape or Chain, 
• Deviation from Standard Length of Chain, 
• Deviation from Standard Temperature; 

And there are formulas for correction for them. 

By using these formulas, we can detect, and applies corrections in Measured Values. By which we get approximate correct value.

Examples

(e = Error, in below examples)

• Measure Value of Angle is 35°. Actual value of same Angle is 36°. So, e = ?

e = 35° - 36° = -1°

• Measured value of Line with a Chain = 50.50 m, Actual value of same line = 50 m, So, e = ?

e = 50.50 - 50 = 0.50 m

• Area of rectangle ABCD measured with Instrument = 201 m², Actual area of rectangle ABCD = 200 m² . So, e = ?

e = 201 - 200 = 1 m²

• Volume of a cube Measured with Instrument using some method = 100.50 m³, Actual volume of same cube = 99 m³ ; So, e = ?

e = 100.50 - 99 = 1.5 m³

• The Height of Tower Measured with Trigonometric Levelling = 30.5 m, Actual value of Height of Tower = 32 m, So, e = ? 

e = 30.5 - 32 = -1.5 m

• Measured distance between two points A and B = 205 m, Actual distance between A and B = 215 m, So, e = ?

e = 205 - 215 = -10 m

• Measured Latitude of a line BD = 10 m , Actual Latitude of Line BD = 11 m, So, e = ?

e = 10 - 11 = -1m

• Actual value of Area of triangle ABC = 500 m², Measured value of Triangle ABC = 480 m², So, e = ?

e = 500 - 480 = 20 m²

• e for a line = 0.5 m, Measured Value of same line = 10 m, So, Actual Value = ?

Actual Value = 10 - 0.5 = 9.5 m

Also See:

Surveying Topics - List of 150+ Topics

Gale's Traverse Table

15+ Surveying Formulas (With some Calculations)