Traversing in Surveying - Principle, Types, Calculations

In this article, we will see about Traversing, some of its Advantages, Instruments, Principles, and various examples of it for Civil Engineers.

So, let's See,

What is Traversing?

Traverse is a set of Connected Lines.

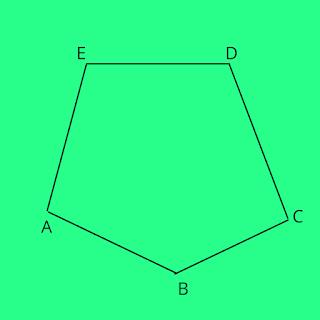Closed Traverse

For Example, in above Line AB is connected with Line BC.

Line BC is connected with Line CD.

We measure distance between stations.

For Example, between point A and of point B, how much distance is there.

And angles.

We start from one point. 

From there to other place, we measure its distance. 

Also, we measure what angles does the line (line which is of point connecting first and second point with North Direction for WCB) make. (Actually, There are different systems of angle measurements. Which types of system of angle measurement do we choose, depends partially on whether it is Open Traverse or Closed Traverse.)

Now, as we have measured distance between first point and second point. And also, angle of it with our system of angle measurement.

We can repeat it for Second Point.

For Second Point, to Third Point, we measure distance between them. 

And what angles does line connecting two stations make.

We again repeat the Same Process Third Point to Forth Point, Forth Point to Fifth Point, and so on, up to last point or last station as we need.

Now, as we have various lines, the length of it, and the values of Angle with system of Angle Measurements we have choose, we can determine given line's Latitude and Departure

Formulas for Latitude and Departure comes handy when we try to find whether we have measured all distances, and angles correctly.

For example,

If we have closed traverse, but end point doesn't exactly meet starting point, then there could be some error. Accordingly we add or substract parts of error to various our Angles and Lengths, such as Traverse becomes fully closed.

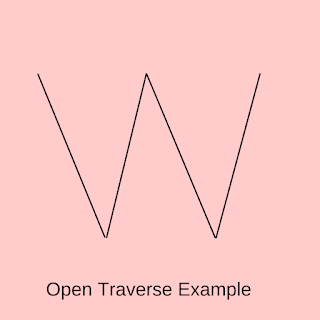
But in Open Traverse, above method of determining error in Angles and Line doesn't work, and therefore we usually don't much use this traverse.

Instruments

Now, as we have to find various Lengths of Lines, and what angle does it makes with North, or what angle does it makes with other lines, we need some Instruments.

So, what Instruments we can use?

We can use some equipment that are specially designed for measuring lengths, and angle in the field.

For example,

• Theodolite

We use Theodolite to measure Angles.

• Total Station

• Prismatic Compass

We can use compass to find North Direction, and what angle is between our line and North Line.

• Tape

We can use Tape to measure Length of Line, or distance between two points.

• Chain

We use Chain in the procedure, to find lengths or distance between two points or stations.

• EDMI

We use EDMI which is an Advanced Instrument to accurately measure distance between two points.

Now, let's see,

Principles of Traversing

• When we measure Angles or Lengths, both of these should have similar degree of precision. And what Equipment do we use, we should also need to take care it. 
• Why? Because Suppose Length we have measured very precisely, but angle is not much precise. Then what will happens. Our work of very precisely measured length, is not of much use, because when we do calculation, we also have less precise quantity with us, which makes calculation not much better.
• Sum of all Angles should be (2N ± 4)*90°.
• For example, if it has four sides, then angle of all parts should be (2*4 - 4)*90° = 360°.
• If sum of Angles deviates from above formula, we need to adjust it, using various methods such as Sum becomes equals to it.
• For a full Closed Traverse, the sum of Latitude and sum of Departures of all Line should be Zero.
• Why? Because as Traverse is closed, means it first point meets last point. And Latitude is projection of N-S axis, so while we are doing sums of Latitude, some will be positive, and some can be negative, depending on in which Quadrant is it compared to North.
• Below Example, should make it clear:
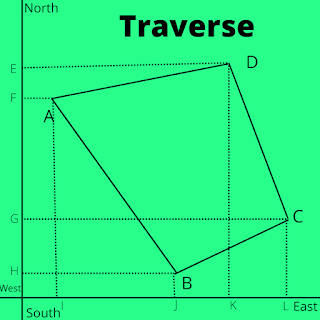
• Traverse ABCD is there.

• Now, let's project its lines AB, BC, CD, and DA on N-S axis.
• But to project it, let's make N-S and E-W axis, such as our traverse comes in first Quadrants.

• Now, as Latitude is projection of given Line on N-S axis, so Let's project it on N-S axis.

• Now latitude of line AB will be = -FH, (minus sign because it is opposite to up direction, which we take as positive)
• Latitude of line BC = GH;
• Latitude of line CD = GE;
• Latitude of line DA = -EF.
• Now, Sum of Latitudes of line AB, BC, CD, and DA will be = (-FH) + GH + GE + (-EF) = (GH + GE) - (FH + EF) = EH - EH = 0
• Similarly, as Departure is projection of E-W axis, its sums also similarly zero in similar way.

• This same can be applies for any number of sides of closed Traverse, like with 5 sides, 6 sides, or 10 sides etc. And Sums of Latitude and Departure for it, will be as by similar calculation above, will be zero, if there is not any errors in length or angle of Traverse..

Advantages of Traversing

• We can find precise Angles, and Length of Line, and if there are some errors in measurements, checks are there by which we can understand and adjust for Error.
• We can Survey Large area.
• We can find Whole Circle Bearing, Quadrantal Bearing or Reduced Bearing of a Line.
• In the Field, we can use it to calculate Latitude and Departure of individual line, from measured distance, and angles, by Formulas.
• If Length of some line, or Angle between lines is missing, we can find it using Trigonometry, and with Other measured lengths, and Angles.

Types of Traverse

Main Two Types of it are there which are as follows:

Open Traverse

Open Traverse is a type in which starting point of station and closing point of station doesn't meet or intersect.

In it, starting point, and ending points generally far away. We can used it when we don't know the exact location of what parts do we have to traverse.

We prefer it for Roads, Railway. As we have seen equipment, we use theodolite or prismatic compass to find angles. For length, we use Chain, Tape, or EDMI. Modern equipment like EDMI helps us to precisely measure long range of distance while consuming compared to less resources in short time.

Closed Traverse

Closed Traverse is a type in which the place of starting, and the place of ending either meets or very close to point of intersecting.

It can be classified into two cases. 

In first case, Starting point Intersect at Ending Point.

For Example:

In this case, Sum of Latitude and Departure of all lines will be Zero.

In Second case, it is very close to point of Intersection.

For Example:

When point is very close to point of Intersection, but doesn't intersect, then there will some values remain while we do sum of the Latitude and Departure of all lines. The remaining value shows how much end point is close to starting point. We can find from it using trigonometry, and by some calculation.

Traverse Calculations

Here's are some Problems related to the topic:

Q (1): A Traverse ABCD consists of Line AB, BC, CD, and DA. Length of Line AB is 60m, Length of Line BC is 60m, Length of Line CD is 60m. And Included Angles of point A, B, C, and D is 90°. So, what will be Length of Line DA?

A: Length of Line DA = 60m

Hint: Use ΣL = 0, and ΣD = 0, where, L is Latitude, and D is Departure which can be calculated using formula,  

Latitude = Length * cos (Angle)

Departure = Length * sin (Angle)

Q (2): A Traverse PQR has lines PQ, QR, and RP. Of which, Length of line PQ is 40m, Length of line QR is 30m. If Angle between Line PQ and QR is 90°. What will be Length of Line RP?

A: 50m

Q (3): A Traverse ABC consists of Line AB, Bc, and CA. Of which Length of Line AB is 80m, Length of Line BC is 80m. Angle between Line AB and BC is 60°. Then what would be Length of Line CA?

A: 80m

Hint: Use simple Trigonometry Formula. See Latitude and Departure Formula from this list of Surveying Formulas.

Related Articles

Gale's Traverse Table

Hypsometric Levelling

Surveying Topics