12+ Surveying Formulas helpful for Civil Engineers
In this article, We will See some of the Important Formulas of Surveying for quick revision and overview of the Subject.
Here's What will We See:
- Direct Vernier Formula
- Least Count Formula
- Retrograde Formula
- Error Formula
- Correction Formula
- Relationship between Error and Correction Formula
- Correction for Slope Formula
- Correction for Temperature Formula
- Correction for Pull Formula
- Relationship between Fore Bearing and Back Bearing Formula
- Latitude Formula
- Departure Formula
- Relative Error of Closure Formula
- Trigonometric Levelling Basic Formula
- Most Probable Error Formula
- Tacheometry Stadia Method Formula
Direct Vernier Formula
where,
s = length of one division on the main scale
n = numbers of divisions on the Vernier scale
v = length of one division on the Vernier
Least Count Formula
where,
s and n are similar as seen above.
We can calculate the Least Count of both Direct Vernier and Retrograde Vernier using the above formula.
Retrograde Vernier Formula
where,
n, v, and s are similar as we have seen.
Error Formula
Problems
Correction Formula
where,
as we have seen in the error formula, True Value is the value that is actually the length of a line or the actual distance between points.
Measured Value is the value which we measure by some instruments like a chain, or tape of a given distance.
Problems
Relationship between Correction and Error Formula
where,
Correction and Error as we have already seen above.
Problems
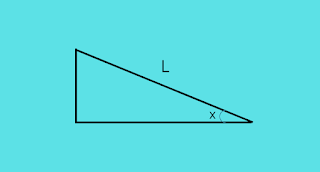
Correction for Slope Formula
where,
as we see in the image, it is an approximate sketch of the slope we encounter on the surface of the earth. If we measure the Slope distance as 'L', and the approximate value of angle as 'x', then the value of correction required to get the horizontal distance such as if slope doesn't exist, is given by it.
Problems
Correction for Temperature Formula
where,
α is the coefficient of thermal expansion
L is the length of distance being measured
Tm is the measured value of Temperature means the value of average temperature during measurement
Ts is the Standard Temperature or reference temperature.
Problems
Correction for Pull Formula
where,
Ps = Standard Pull of Tape
Pm = Measured Pull of Tape
L = Measured Length of Tape
A = Cross Section Area of Tape
E = Modulus of Elasticity of Tape
Derivation
Change in length for pull is = (-)PL/(AE).
Now, as we find a correction for pull, we have to find how much we need to add in Measured Pull to obtain Standard Pull or Correct value of Pull. Now, for Standard pull is (-)PsL/(AE) and the Measured pull is (-)PmL/(AE).
So, correction is = (-)PsL/(AE) - (-)PmL/(AE) ; which is = (Pm - Ps)L / (AE)
And how does the Change in length formula derived? It comes from the definition of modulus of elasticity, which is
(Modulus of elasticity) = (Stress)/(Strain)
Now, (Stress) = (Force)/(Area); and (Strain) = (Change in Length)/(Original Length)
So, (Modulus of Elasticity) = ((Force)/(Area))/((Change in Length)/(Original Length));
which is = (Force)*(Original Length)/(Area)*(Change in Length);
So, (Change in Length) = (Force)*(Original Length)/(Area)*(Modulus of Elasticity)
And we give a minus sign in a case for the pull because it is opposite to what the sign is during Stress.
Problems
Relationship between Fore Bearing and Back Bearing Formula
where,
Back Bearing is the clockwise angle measured of the line in the opposite direction in which the survey was carried out.
Fore Bearing is the clockwise angle measured of the line in the same direction in which the survey was carried out.
Whole Circle Bearing is the system of measurement of angle in which we measure angle clockwise from North Direction, and measure complete angle even if it exceeds 180 degrees. As it is measured from 0 degrees to 360 degrees, like a complete circle, it is called Whole Circle Bearing.
Quadrantal Bearing is the system of measurement of angle in which we measure angle either clockwise or anti-clockwise depending upon whether a measurement is in which quadrants, and it doesn't always measure from only North Direction, but North Direction and South Direction depending upon it are in which part of Quadrants. For Example, if Angle is in the first Quadrant, we measure clockwise from North Direction.
If Angle is on the second Quadrant (Here, the Second Quadrant is below the First Quadrant instead of being left to it), then we measure it from South Direction and anti-clockwise such as the angle remains less than or equal to 90 degrees.
Similarly, if Angle is in Third Quadrant, we measure it from South Direction but clockwise, and write the direction to it like it is between the South and West direction, So, the angle is written as "S45W". And if Angle is in the fourth Quadrant, we measure it from North Direction but Anti-Clockwise and write as an example, "N25W".
Problems
Q (1): For Whole Circle Bearing, what is the Difference between Fore Bearing and Back Bearing (in absolute number)?
A: 180
Q (2): For Quadrantal Bearing system, angle is "N45E", then what will be this angle in Whole Circle Bearing System?
A: 45 degrees
Hint: Here "N45E" means angle is in First Quadrant, therefore WCB would be equals to QB.
Latitude Formula
where,
L is the Latitude of a line, which is a projection of a line in a North-South direction
l is the length of the line
x is an Angle of line in a Quadrantal Bearing System
Problems
Departure Formula
where,
D is the Departure of a line, which is a projection of a given line in an East-West Direction
l is the length of the line
x is an Angle of line in a Quadrantal Bearing System
We use above Formulas in Traversing problems.
Relative Error of Closure Formula
where,
Relative Error of Closure is the quantity that gives the value of how much error of closure is there given the perimeter of the traverse.
An error of Closure is a total error that remains between if the traverse was completely closed and where the traverse is now.
The perimeter of the Traverse is the sum of all lengths given traverse.
This formula is used in traversing, specifically in problems of the closed traverse, where some error remains such as the first point of traverse has not met its endpoints.
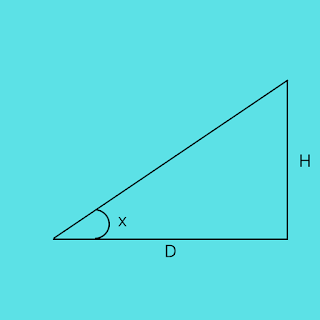
Trigonometric Levelling Basic Formula
where,
H is the Height of a Tower or Mountain required to find.
D is the Horizontal distance from a point to a given object.
x is the angle made by an object from a point from where horizontal distance is being measured and the top of the object, the height of which is determined.
Problems
Q (1): If horizontal distance between Object and Tower is 15m, and angle it makes with top of tower, from starting point of distance is 45 degrees, then what will be height of tower?
A: 15m
Hint: tan 45 = 1
Q (2): If height of Tower is 20m, and Horizontal Distance from tower to point where angle being made is 34.64m, then what angle will it make with top of Tower?
A: 30 degrees
Hint: As H = D tan x; tan x = (H/D); Put the values of H and D; and find x angle.
Q (3): If Height of Mountain is 100m, and angle to top of Mountain from starting point of leveling is 45 degrees, then what is the Horizontal Distance between starting point of levelling and Mountain?
A: 100m
Hint: As H = D tan x; therefore D = (H)/(tan x); put the values of H and x.
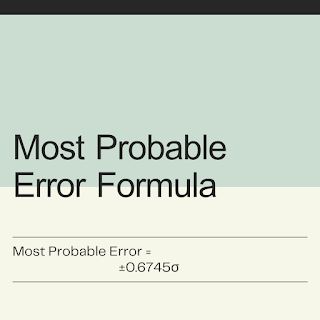
Most Probable Error Formula
Problems
Q(1): Standard Deviation for given set of errors has 1. What will be the Most Probable Error?
A: ±0.6745
Q (2): Most Probable Error for given set of Errors is 1. What would be Standard Deviation?
A: ±1.4826
Q (3): What is the ratio of Most Probable Error to Standard Deviation for given values of Errors?
A: ±0.6745
Tacheometry Stadia Method Formula
where,
D is the Distance between the point where Tacheometer is there and of point where staff is there.
K is the constant of Multiplication also known as Multiplying Constant.
C is Constant of addition in formula, also called additive constant..
s is the Staff Intercept or the distance between two points on staff which can be seen from Telescope.
Problems
Q (1): If K is 100, C is 0, and s is 2m, then what would be distance between staff and oint of Instrument?
A: 200m
Hint: Use D = Ks + C; Put values, so D = (100)*(2) + 0 = 200m
Q (2): If D is 150m, K is 100, and C is 0, then what would be Staff Intercept of given Staff?
A: 1.5m
Hint: As
D = Ks +C;
s = (D - C)/(K);
Put values, So:
s = (150 - 0)/(100)
So, s = 1.5m
Q (3): If K= 100, D = 200m, s = 1.9m; then what would be additive constant C of given Instrument?
A: 10
Hint: As, Ks + C = D;
So,
C = D - Ks;
Now, putting values;
C = (200 - (100)*(1.9))
C = (200 - 190)
C = 10
Conclusion
As we have seen various Surveying Formulas, try to practice them using various examples. You can even make an example yourself, and try to solve it.





















Comments
Post a Comment